滤波算法
in 机械/电子/内核
快速目录
均值滤波(ADC为例,用于电源检测)
往往就是ADC通过中断取若干值,然后求平均,这种滤波较简单,下面只附代码
uint16_t voltbuf[5] = {4095,4095,4095,4095,4095};
extern ADC_HandleTypeDef HADC;
uint8_t Check_volt(uint16_t *volt)
{
uint8_t i,cnt=0;
uint32_t vol = 0;
static uint32_t time_next = 0;
uint32_t time_curr = HAL_GetTick();
if(time_curr >= time_next)
{
HAL_ADC_Start_IT(&HADC);
time_next = time_curr + BAT_PERIOD;
}
for(i=0;i<5;++i)
{
vol += voltbuf[i];
if(voltbuf[i] < BAT_TH)
++cnt;
}
*volt = vol / 5;
if(cnt >= 3)
return 0xff;
else
return 0;
}
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef* hadc)
{
static uint8_t i = 0;
voltbuf[i] = HAL_ADC_GetValue(hadc);
i = (i==5? 0:++i);
}
低通滤波(常用于飞控油门)
低通滤波可以简单的认为:设定一个频率点,当信号频率高于这个频率时不能通过,在数字信号中,这个频率点也就是截止频率,当频域高于这个截止频率时,则全部赋值为0。因为在这一处理过程中,让低频信号全部通过,所以称为低通滤波。
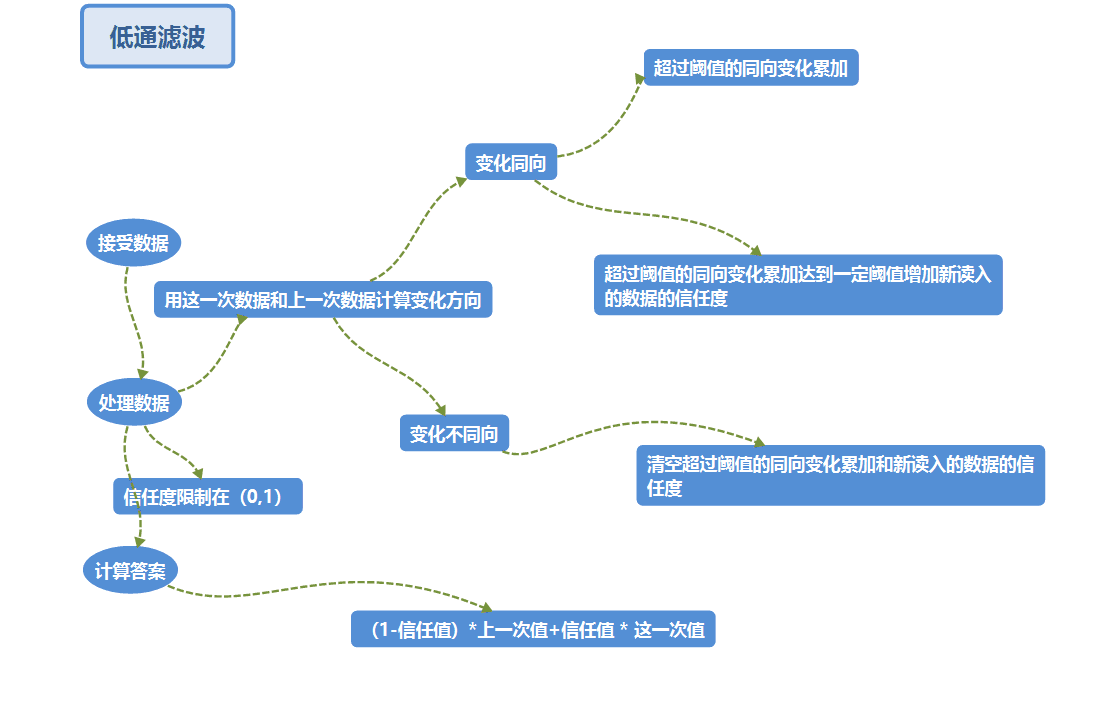
更新参数的一阶低通滤波算法流程
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
using namespace std;
float filter(float data_N)
{
static int limit1 = 8;
static int limit2 = 5;
static int num = 0;
static float trust= 0.2;
static int flag_N = 0, flag_L = 0;
static float data_L = 0;
flag_N = (data_N - data_L > 0)?1:0;
if (flag_L == flag_N)
{
if (abs (data_N - data_L) > limit1)
num += 5;
if (num >= limit2)
trust += 0.1;
}
else
{
num = 0;
trust = 0.2;
flag_L = flag_N;
}
if (trust > 0.99) trust= 0.99;
data_N = (1-trust) * data_L + trust * data_N;
data_L = data_N;
return data_N;
}
int main()
{
freopen("time.txt","r",stdin);
freopen("filter.txt","w",stdout);
float f;
for(int i = 1; i<= 100; i++)
{
scanf("%f,",&f);
printf("%.2f,",filter(f));
}
return 0;
}
步兵评测:
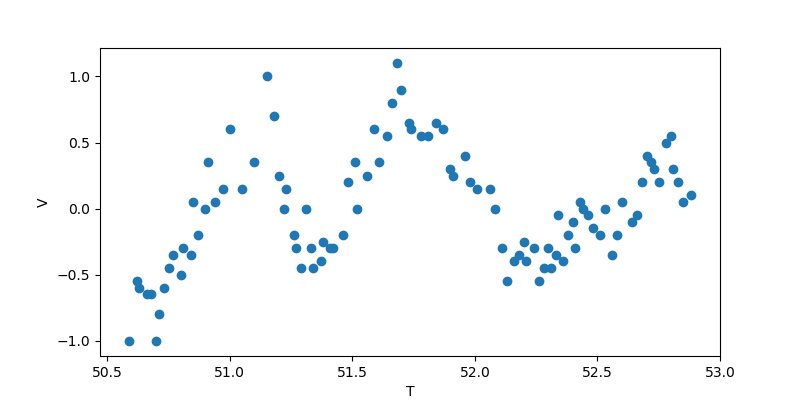
滤波前
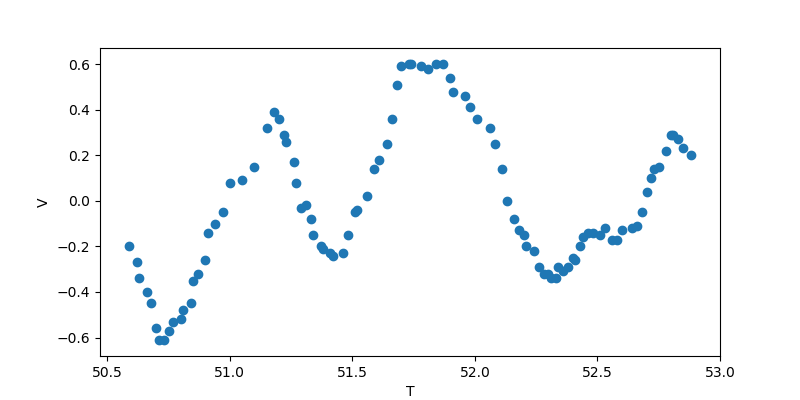
滤波后
中通滤波
滑动平均滤波算法只采样一次,将一次采样值和过去的若干次采样值一起求平均,得到的有效采样值即可投入使用。如果取N个采样值求平均,存储区中必须开辟N个数据的暂存区。每新采集一个数据便存入暂存区中,同时去掉一个最老数据,保存这N个数据始终是最新更新的数据。采用环型队列结构可以方便地实现这种数据存放方式。
#include<iostream>
#include<memory.h>
using namespace std;
typedef double element;
void medianFiltering(const element * signal, element * result, int N)//中值滤波函数,signal初始数据,result最终输出数据,N初始数据长度
{
const int n = 5;//窗口大小为5,窗口大小为奇数
element window[n];//储存窗口排序数据
for(int i=n/2; i<N-n/2; i++)
{
for(int j=0; j<n; j++)
{
window[i] = signal[i-n/2+j];
}
for(int j=0; j<=n/2; j++)//因为只需要用到中值,所以只排一半就好
{
for(int k=j+1; k<n; k++)
{
if(window[j]>window[k])
{
swap(window[j], window[k]);
}
}
}
result[i-n/2] = window[n/2];
}
}
void boundary(element * signal, element * result, int N)//处理边界,即扩充边界
//注释:建议写成vector,这个标称太丑陋
{
const int n = 5;
if(!signal || N<1)
{
return;
}
if(N==1)
{
if(result)
{
result[0]= signal[0];
}
return;
}
element * extension = new element[N+n-1];
if(!extension)
{
return;
}
memcpy(extension+n/2, signal, N*sizeof(element));//将原数据复制到扩充数组中
for(int i=0; i<n/2; i++)
{
extension[i] = signal[n/2-1-i];
extension[N+n/2+i] = signal[N-1-i];
}
medianFiltering(result?extension:signal, result, result?N+n-1:N);
delete []extension;
}
卡尔曼滤波
根据当前的仪器”测量值” 和上一刻的 “预测量” 和 “误差”,计算得到当前的最优量. 再 预测下一刻的量,
unsigned long now = millis(); //当前时间(ms)
dt = (now - lastTime) / 1000.0; //微分时间(s)
lastTime = now; //上一次采样时间(ms)
accelgyro.getMotion6(&ax, &ay, &az, &gx, &gy, &gz); //读取六轴原始数值
float accx = ax / AcceRatio; //x轴加速度
float accy = ay / AcceRatio; //y轴加速度
float accz = az / AcceRatio; //z轴加速度
aax = atan(accy / accz) * (-180) / pi; //y轴对于z轴的夹角
aay = atan(accx / accz) * 180 / pi; //x轴对于z轴的夹角
aaz = atan(accz / accy) * 180 / pi; //z轴对于y轴的夹角
aax_sum = 0; // 对于加速度计原始数据的滑动加权滤波算法
aay_sum = 0;
aaz_sum = 0;
for(int i=1;i<n_sample;i++)
{
aaxs[i-1] = aaxs[i];
aax_sum += aaxs[i] * i;
aays[i-1] = aays[i];
aay_sum += aays[i] * i;
aazs[i-1] = aazs[i];
aaz_sum += aazs[i] * i;
}
aaxs[n_sample-1] = aax;
aax_sum += aax * n_sample;
aax = (aax_sum / (11*n_sample/2.0)) * 9 / 7.0; //角度调幅至0-90°
aays[n_sample-1] = aay; //此处应用实验法取得合适的系数
aay_sum += aay * n_sample; //本例系数为9/7
aay = (aay_sum / (11*n_sample/2.0)) * 9 / 7.0;
aazs[n_sample-1] = aaz;
aaz_sum += aaz * n_sample;
aaz = (aaz_sum / (11*n_sample/2.0)) * 9 / 7.0;
float gyrox = - (gx-gxo) / GyroRatio * dt; //x轴角速度
float gyroy = - (gy-gyo) / GyroRatio * dt; //y轴角速度
float gyroz = - (gz-gzo) / GyroRatio * dt; //z轴角速度
agx += gyrox; //x轴角速度积分
agy += gyroy; //x轴角速度积分
agz += gyroz;
/* kalman start */
Sx = 0; Rx = 0;
Sy = 0; Ry = 0;
Sz = 0; Rz = 0;
for(int i=1;i<10;i++)
{ //测量值平均值运算
a_x[i-1] = a_x[i]; //即加速度平均值
Sx += a_x[i];
a_y[i-1] = a_y[i];
Sy += a_y[i];
a_z[i-1] = a_z[i];
Sz += a_z[i];
}
a_x[9] = aax;
Sx += aax;
Sx /= 10; //x轴加速度平均值
a_y[9] = aay;
Sy += aay;
Sy /= 10; //y轴加速度平均值
a_z[9] = aaz;
Sz += aaz;
Sz /= 10;
for(int i=0;i<10;i++)
{
Rx += sq(a_x[i] - Sx);
Ry += sq(a_y[i] - Sy);
Rz += sq(a_z[i] - Sz);
}
Rx = Rx / 9; //得到方差
Ry = Ry / 9;
Rz = Rz / 9;
Px = Px + 0.0025; // 0.0025在下面有说明...
Kx = Px / (Px + Rx); //计算卡尔曼增益
agx = agx + Kx * (aax - agx); //陀螺仪角度与加速度计速度叠加
Px = (1 - Kx) * Px; //更新p值
Py = Py + 0.0025;
Ky = Py / (Py + Ry);
agy = agy + Ky * (aay - agy);
Py = (1 - Ky) * Py;
Pz = Pz + 0.0025;
Kz = Pz / (Pz + Rz);
agz = agz + Kz * (aaz - agz);
Pz = (1 - Kz) * Pz;